Extracting The DC Component
|
If you integrate over the full period of a sinusoid, the area found will be zero. This is also true if you integrate over the full period (fundamental wavelength) of a complex periodic wave that is composed only of sinusoids. The diagram below shows this.
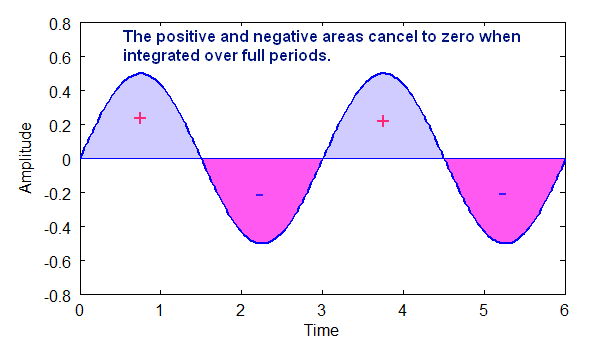
Above: Diagram shows how the area of a sine wave is zero when integrated over whole periods.
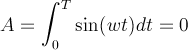
The area above the x-axis is positive area and the area below the x-axis is negative area. For a sinusoid the total area over one or more periods is always zero.
So, if there is no DC component in a complex, periodic wave, the area over the period of that wave will be zero.
If there is a DC component, however, then there will be a non-zero (positive or negative) area over that period.
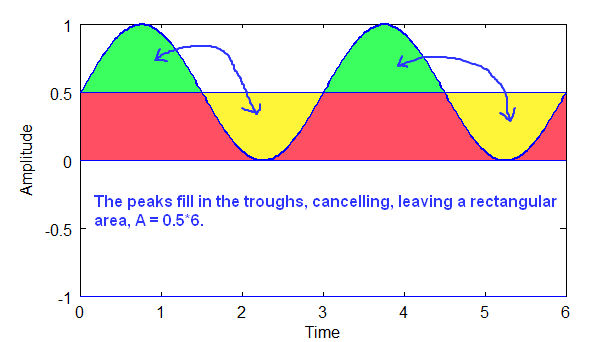
Above: Diagram shows how sinusoidal components cancel, and the remaining area is the DC part, a rectangle.
Given that T is the period of the wave, and A is the area of the DC component rectangle, the coefficient a0 is A/T. The DC component is 0.5 in the diagram above, which is the area divided by the period. In the example above, integration is over two full periods. All of the sinusoidal parts cancel to zero, so they can be ignored!
|

