Periodic Wave Components Are Integer Multiples of The Fundamental
|
The fundamental frequency is the frequency of a periodic wave's repeating pattern, or how long its wavelength is. Below is a complex periodic wave composed of two simple sinusoids. Sinusoid 'A' has wavelength of 3 units (the units are immaterial for this discussion) and sinusoid 'B' has a wavelength of 2 units'. The composition of A and B, wave C, results in a wavelength of 6 units. That is, those two waves in combination create a fundamental wavelength of 6.
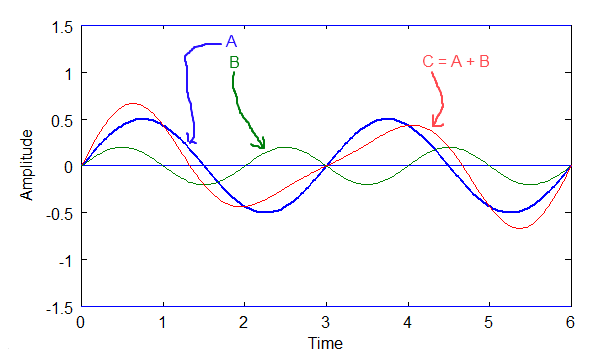
Above: Diagram of C=A+B. A and C are integer multiples of C
Notice that the sinusoidal components of C must be integer multiples of C's frequency. This is necessary if the wave is to be periodic, otherwise the pattern would not repeat. So, the physics of periodic waves makes this necessary. The math to check this is simple, so it might be a good exercise for you to try it yourself.
This is why the composite waves of a periodic wave must be integer multiples of the fundamental frequency,f. So, in the diagram above, A's frequency is 2*f, B's is 3*f, and C's = f. Remember, A and B are what give rise to C.
Brief Foray into the Fourier Transform
A Fourier Transform builds on the basic idea of the Fourier Series. A Fourier Transform allows us to describe non-periodic (and periodic) waves. These are waves that do not have a repeating pattern. I'll show how to derive this after the Fourier Series is more fully described, but order of learning requires the Fourier Series be understood first.
|

