The Superposition Principle
|
Waves travel as sinusoids or as a set of sinusoids.
The diagram below is a simple sinusoidal wave. A sinusoidal wave is the simplest wave possible. The diagram is of a sine wave.
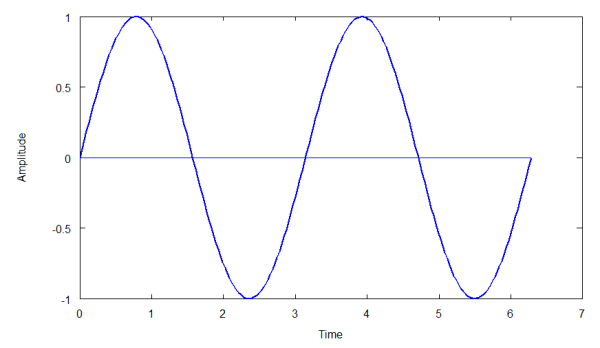
This wave is the same shape as the simple harmonic motion you see in a mass-spring system and for the same reason. The system oscillates around an equilibrium point describing a sine wave as a graph of time versus displacement. With a sound wave (pressure wave), the air compresses and expands (rarifies) around an equilibrium pressure.
A sinusoid is described by three elements: an amplitude, a frequency and a phase. The wave above can be described by "a sin(wt + ph)", where 'a' is the wave's amplitude, 'w' is the angular frequency (so many radians per second), 't' is the time, and ph is the phase shift, or how far from the y-axis the wave starts. In the above case ph = 0.
[TODO: diagram of a spring mass system]
Complex Waves
Complex waves are the composition of two or more sinusoids of varying frequency, amplitude and phase. The diagrams below show two simple sinusoids, 'A' and 'B', each of different amplitude and frequency (phase is the same). 'C' is the composition, or sum, of 'A' and 'B', i.e. C = A + B. C is a complex wave, because it is made up of two sinusoids.
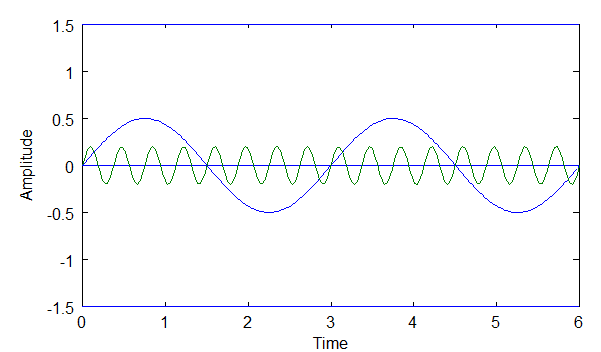
Above: diagram of sine waves A and B.
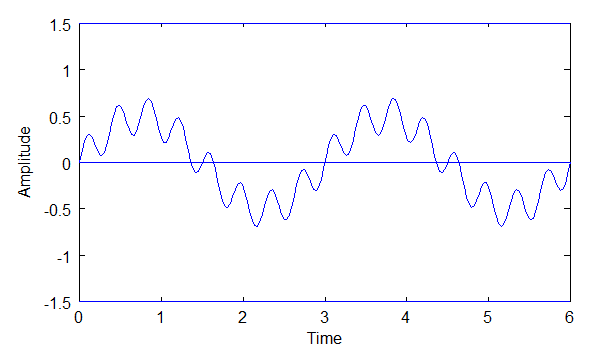
Above: diagram of sine wave C, where C = A+B.
The diagram of C reflects the Superposition Principle, which states that two or more sine waves can traverse the same path at the same time in a medium and when they do they do not interfere with each other. In other words, both waves are still there and each can be extracted from the complex wave.
|

