The Fourier Series Equation
|
Reproducing the diagrams for the Superposition Principle below, let's see how a complex wave can be described.
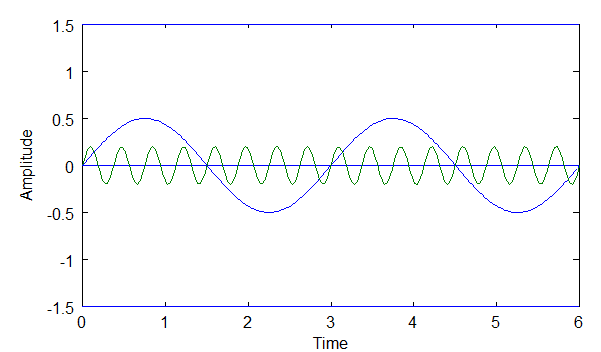
Above: Diagram of sine waves A and B.
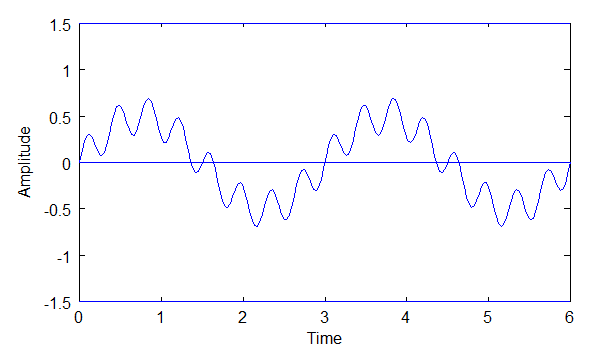
Above: Diagram C, where C = A + B.
From the diagrams above we know that C = A + B. Also, A = 0.5 * sin(2wt), and B = 0.2 * sin(16wt). So, if f(t) represents the complex wave, then:
Equation 1
Equation 1 is wave C represented by a Fourier Series.
Note, the 'w' is the "angular frequency", usually given in radians per second. 'w = 2*pi*f0', where f0 is the fundamental frequency of the wave. Notice that wave A has a frequency twice the fundamental ( 2wt ) and wave B has 16 times the frequency of the fundamental (16wt).
Phase Shift, ph
Phase shifts must also be handled, because a sinusoid can be shifted along the x-axis. If wave A above were shifted by, say, 90 degrees, or pi/2, then the results would look as follows:
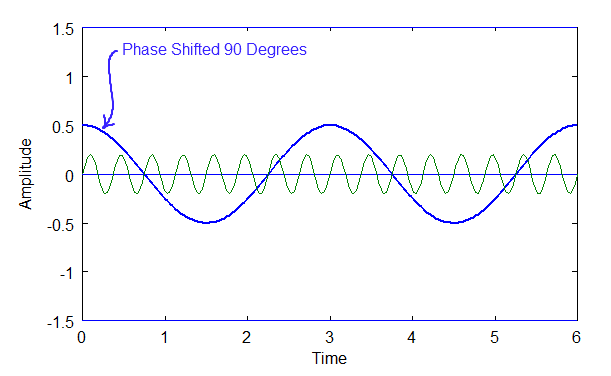
Above: Diagram of two waves, A and B, one phased shifted, A.
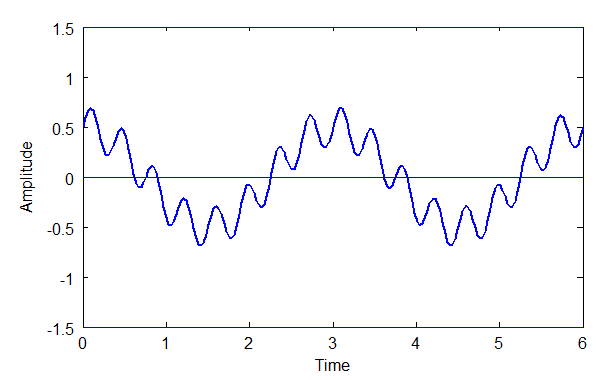
Above: Diagram of C, where C = A + B.
Phase shifting doesn't affect the fundamental frequency. It only affects the wave's shape.
Equation 2
The DC Components
A wave can also have a constant or DC component or signal that shifts a sinusoid up or down the y-axis so that it no longer oscillates around y = 0. The term "DC" comes from "direct current". It's an artifact of electronics, due to the fact that Fourier is often used in dealing with electrical signals. However, DC in Fourier does not have to be an electrical signal. It's just the constant part of any signal, regardless of whether or not the medium is electric, electromagnetic, pressure, etc.
Below are is a DC component, A, and sinusoid B, and the composition of both to produce wave C, which is simply the shifting upward of B.
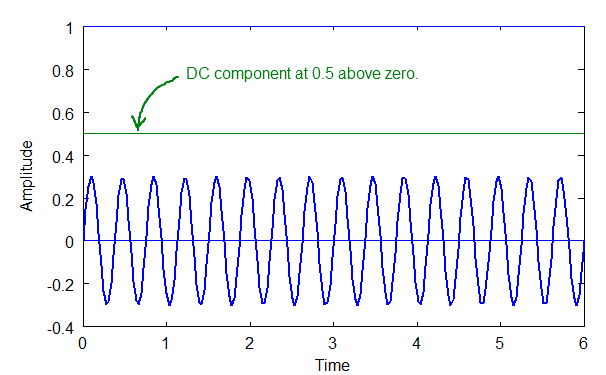
Above: A DC Component, 'A', and a sine wave, 'B'.
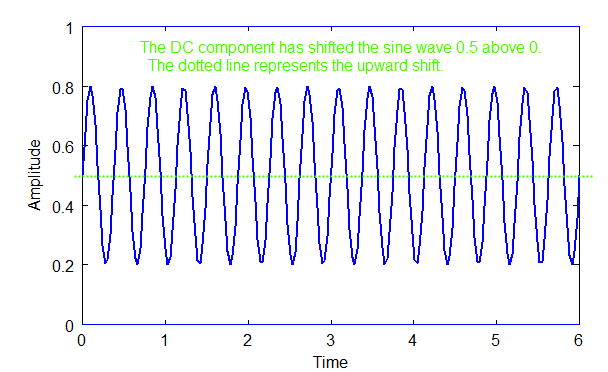
Above: diagram of C = A + B.
The equation for the complex wave, C, above would be:
Equation 3
The General Form of the Fourier Series
First a brief summary of what we've learned so far. The Fourier Series applies only to periodic waves. All of the components of a periodic waves are integer multiples of the fundamental frequency. We also know that each component has its own phase and amplitude. We also must account for a DC component if it exists. Assembling these facts, here is the general form of the Fourier Series:
Equation 4
where a0 is the DC component, and w = 2*pi*f and f = the fundamental frequency.
A More Common Representation of the Fourier Series
More often the Fourier Series is represented by a sum of sine and cosine waves (and often as complex notation, e^jwt. I'll get to that later). I believe the reason for this is because deriving the coefficients in this form is easier. Here is the form:
Equation 5
This form eliminates the phase.
The equation 5 is made possible by the trigonometric identity shown in equation 6, below.
Equation 6
Note, a "wave component", or sinusoid, can be referred to as a "harmonic" or "partial".
|

